Cross Product Of 2 3x1 Matrices

If a and b are matrices or multidimensional arrays then they must have the same size.

Cross product of 2 3x1 matrices. Viewed 7k times 0 begingroup i m not sure how the matrix multiplication at the second image works is it a typo or is my understanding of matrix multiplication flawed. By using this website you agree to our cookie policy. The cross product a b of two vectors is another vector that is at right angles to both. And the vector we re going to get is actually going to be a vector that s orthogonal to the two vectors that we re taking the cross product of.

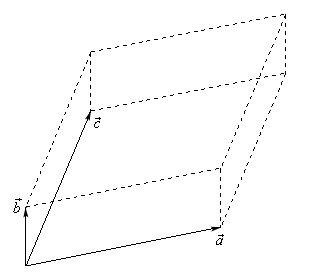
The direction of c follows the right hand rule in turning from a to b. But in the cross product you re going to see that we re going to get another vector. The 3x3 cross product block computes cross or vector product of two vectors a and b the block generates a third vector c in a direction normal to the plane containing a and b with magnitude equal to the product of the lengths of a and b multiplied by the sine of the angle between them. The cross product of two vectors a and b is defined only in three dimensional space and is denoted by a b.

Ask question asked 3 years 11 months ago. Active 3 years 11 months ago. The dot product results in a scalar. The cross product a b is defined as a vector c that is perpendicular orthogonal to both a and b with a direction given by the right hand rule.

The magnitude length of the cross product equals the area of a parallelogram with vectors a and b for sides. In linear algebra the outer product of two coordinate vectors is a matrix if the two vectors have dimensions n and m then their outer product is an n m matrix. The outer product of tensors is also referred to as their tensor product and can be used to define the tensor algebra. In this final section of this chapter we will look at the cross product of two vectors.

More generally given two tensors multidimensional arrays of numbers their outer product is a tensor. Matrix multiplication question of 2 3x1 vectors. Two vectors can be multiplied using the cross product also see dot product. We should note that the cross product requires both of the vectors to be three dimensional vectors.

If a and b are vectors then they must have a length of 3. In this case the cross function treats a and b as collections of three element vectors. Also before getting into how to compute these we should point out a major difference between dot products and cross products. Free vector cross product calculator find vector cross product step by step this website uses cookies to ensure you get the best experience.

The cross product is defined as follows. You take the dot product of two vectors you just get a number. The function calculates the cross product of corresponding vectors along the first array dimension whose size equals 3.